Do We Really Need Model Compression?

Model compression is a technique that shrinks trained neural networks. Compressed models often perform similarly to the original while using a fraction of the computational resources. The bottleneck in many applications, however, turns out to be training the original, large neural network before compression. For example, BERT-base can be trained on a consumer GPU (12 GB of memory) but BERT-large needs to be trained on a Google TPU (64 GB of memory), which prevents many people from experimenting with pre-training language models.¹

Results from the field of model compression tell us that the solutions we converge to usually have far fewer parameters than the models we originally train.

So what’s stopping us from saving GPU memory by training small models from scratch?

In this blog post, we’ll explore the obstacles involved in training small models from scratch. We’ll discuss why model compression works and two approaches to memory-efficient training: over-parameterization bounds and better optimization methods, which may reduce or eliminate the need for post-hoc model compression. We’ll wrap up with future research directions.

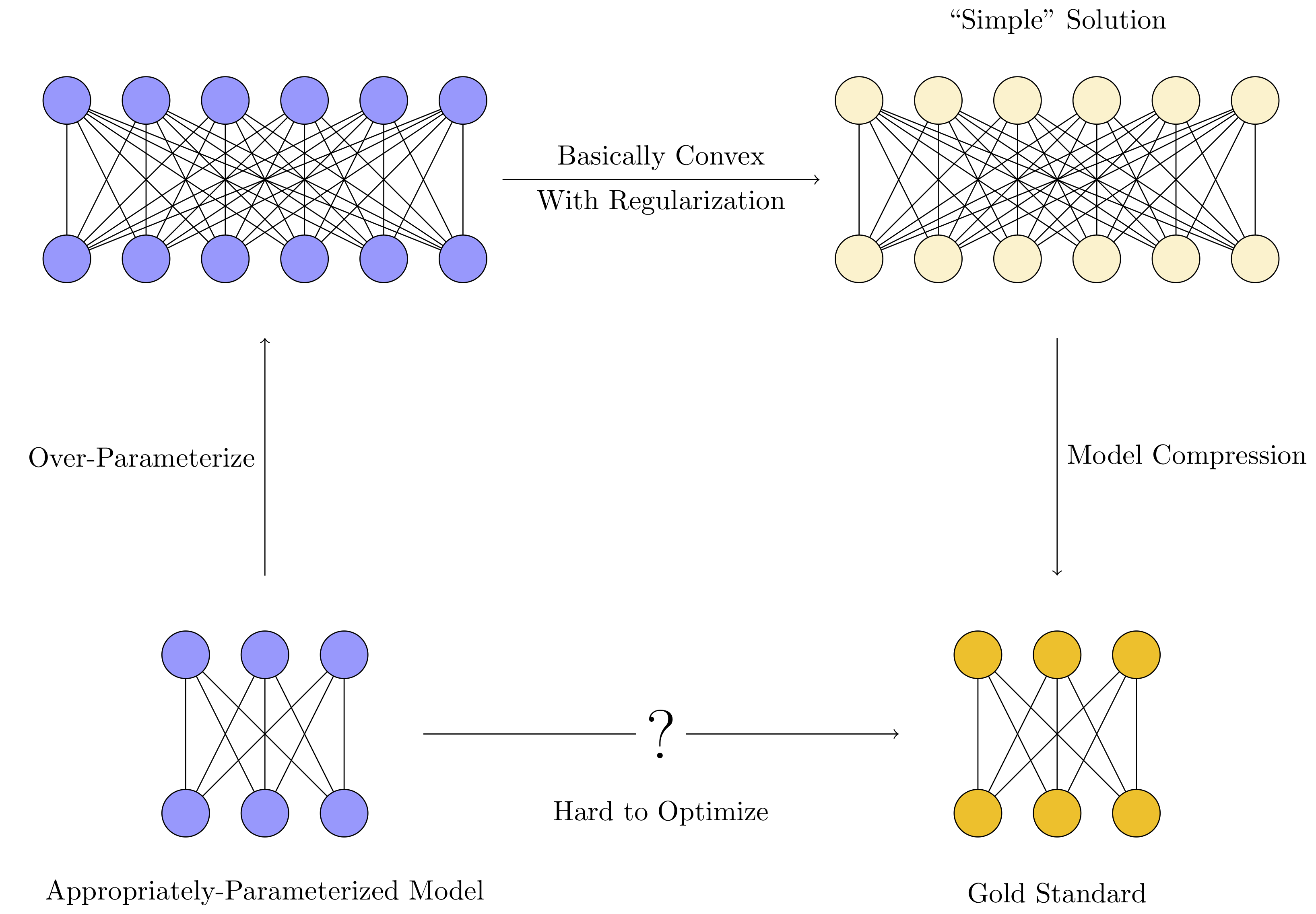
Appropriately-Parameterized Models

Appropriately-Parameterized Model (noun) - A model that is neither over-parameterized nor under-parameterized, but has exactly the right amount of parameters to represent the ideal solution for a task.

We don’t typically train appropriately-parameterized models in the deep learning paradigm. This is because the appropriate number of parameters is usually not known for a given dataset. Even when the solution is known, appropriately-parameterized models are notoriously difficult to train using gradient descent.²

Instead, the training procedure typically looks like this:

An over-parameterized model is trained instead. These models usually have many more parameters than the number of training examples.
Various regularization techniques (implicit or otherwise)³ are used to constrain optimization to prefer “simple solutions” rather than over-fitting.
Model compression extracts the “simple” model embedded inside the larger one by eliminating redundancies, bringing memory and time efficiency closer to that of the ideal appropriately-parameterized model.

Extreme over-parameterization makes training much easier. Because the models are over-parameterized, however, they can memorize the data⁴ instead of learning useful patterns in the data, which necessitates the regularization. Model compression then exploits this simplicity to only keep the parameters that were actually needed for the solution.

Since our objective is to train neural networks using less GPU memory, there are some obvious questions we can ask:

Why is over-parameterization necessary? How much over-parameterization is needed?
Can we reduce over-parameterization by using smarter optimization methods?

The next two sections will address these questions in turn.

Over-parameterization Bounds

Why is over-parameterization necessary? By sufficiently over-parameterizing our neural networks, we make the optimization landscape effectively convex. Du et al. (2019)⁵ and Haeffele and Vidal (2017)⁶ proved this mathematically for some simple cases, giving the necessary amount of over-parameterization to achieve 0 training loss in polynomial time. Effectively, over-parameterization is trading computational intractability for more memory usage.

These bounds are generally considered to be loose. This means that while we can predict a sufficient number of parameters to fit some data perfectly, we still don’t know the minimum number of parameters required to fit the data perfectly. Tight bounds will likely depend on everything from the optimization procedure (SGD vs. GD, Adam vs. Others) to the architecture. Computing a tight bound might even be more computationally intractable than training all the possible candidate networks.

But there’s definitely still room for improvement in this area.⁷ Tighter over-parameterization bounds would let us train smaller networks without grid searching over architectures or worrying that a bigger network might give us better performance. Extensions of the proofs to recurrent models, transformers, models trained with batch norm, etc. are also still in question.

Edit (2/2/20): I neglected to mention that different architectures will probably have different over-parameterization bounds. A reasonable approach then is to use a different architecture that has a lower over-parameterization bound. Some interesting “efficient transformers” include the Reformer, ALBERT, Sparse Transformers, and SRUs.

Better Optimization Techniques

Empirically, appropriately-parameterized models are difficult to train. Training an appropriately-sized model with gradient descent will typically fail spectacularly. The model won’t converge to fit the training data, let alone generalize well. This is partially explained by the non-convexity / non-friendliness of the optimization landscape of neural networks, but a precise characterization of the computational complexity of training appropriately-parameterized models remains incomplete.⁸

Model compression techniques give us a hint about how to train appropriately-parameterized models by elucidating the types of solutions over-parameterized models tend to converge to. There are many types of model compression, and each one exploits a different type of “simplicity” that tends to be found in trained neural networks:

Many weights are close to zero (Pruning)
Weight matrices are low rank (Weight Factorization)
Weights can be represented with only a few bits (Quantization)
Layers typically learn similar functions (Weight Sharing)

Each of these “simplicities” are either induced by regularization during training (implicit or otherwise)³ or by the quality of the training data. When we know we’re looking solutions with these properties, it opens up exciting new directions for improving our optimization techniques.

Sparse Networks from Scratch

Weight pruning is the probably the most successful example of a compression method turning into an optimization improvement. Trained neural networks typically have many weights (30 - 95%) that are close to 0. These weights can be removed without affecting the output of the neural network.

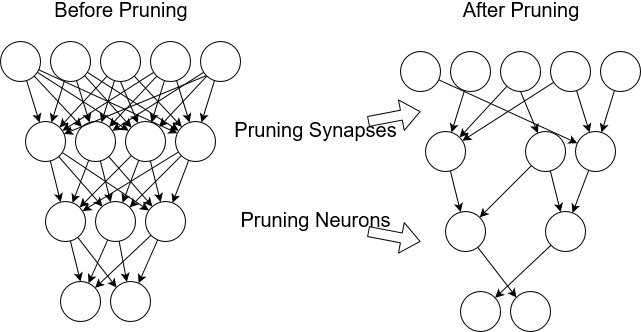
Source

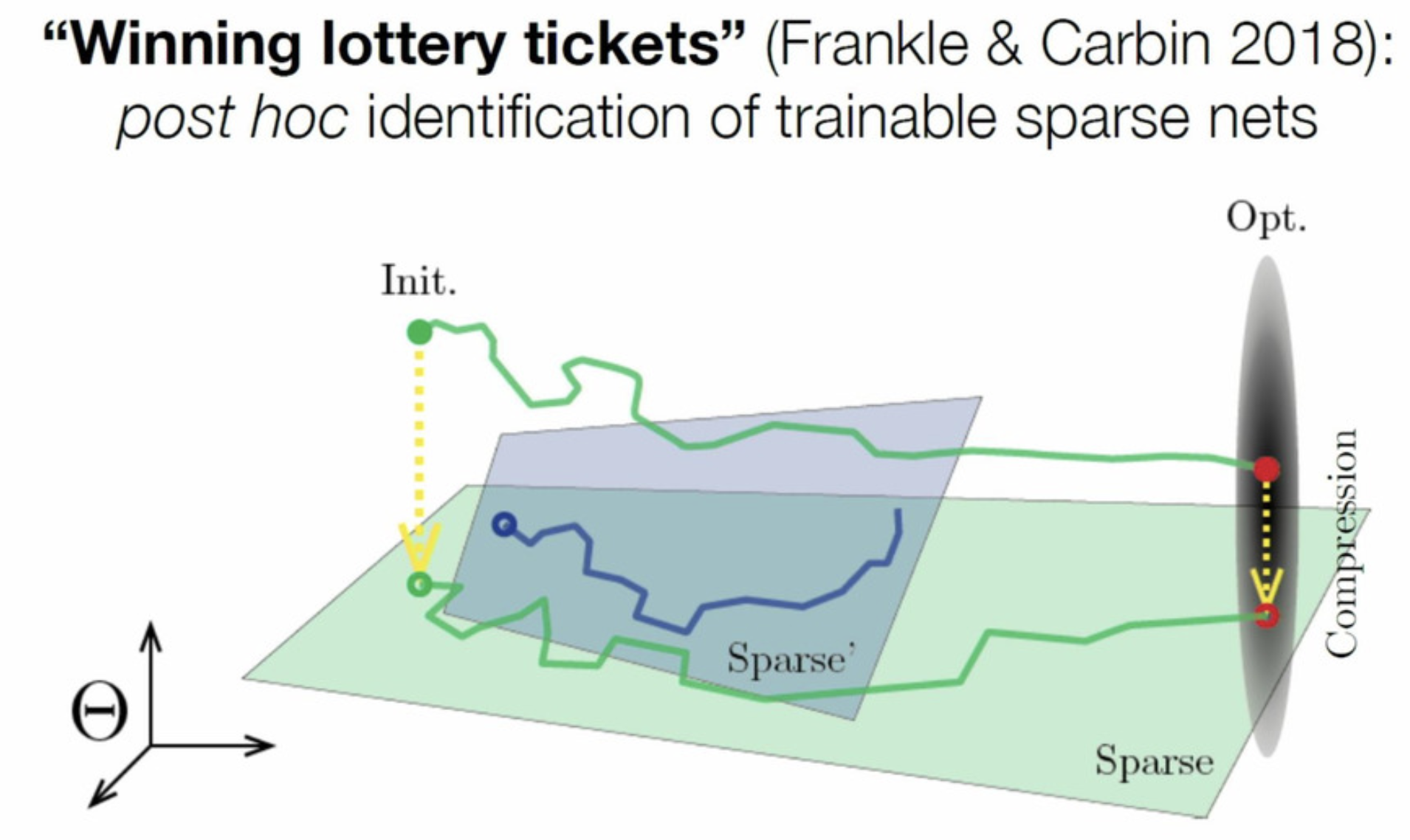
Can we reduce GPU usage by training sparse neural networks from the beginning, rather than pruning post-hoc? For a while, we thought the answer was no. Sparse networks are difficult to train; the optimization landscape is very non-convex and unfriendly.

However, Frankel and Carbin (2018)⁹ took the first step in that direction. They found they could re-train the pruned network from scratch, but only if it was re-initialized to the same initialization used during dense training. Their explanation for this is the Lottery Ticket Hypothesis: the dense network is actually a randomly initialized combination of many appropriately-parameterized sparse models in parallel. One happens to get a lucky initialization and converge to the solution.¹⁰

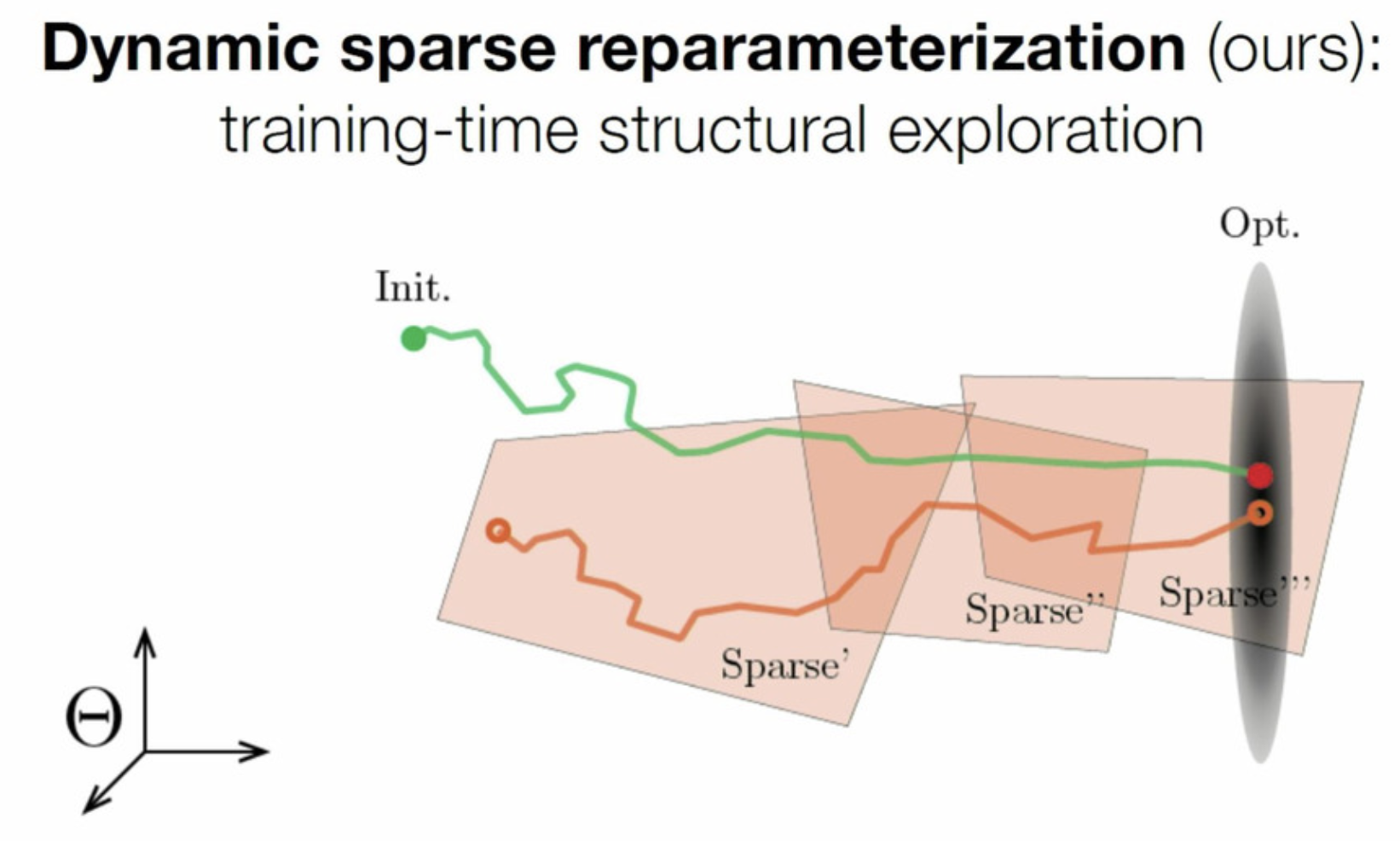
Parameter efficient training of deep convolutional neural networks by dynamic sparse reparameterization

Most recently, Dettmers and Zettlemoyer (2019)¹¹, Mostafa et al. (2019)¹², and Evci et al. (2019)¹³ have shown that appropriately-parameterized sparse networks can be trained from scratch, greatly reducing the amount of GPU memory needed to train neural networks. The important thing isn’t the initialization, but the ability to explore the sparse subspace of the model. Similar work by Lee et al. (2018)¹⁴ attempts to find the appropriate sparse architecture quickly by doing a single pass over the data.

I believe this pattern will likely be repeated with other types of model compression. More generally the pattern is:

Model compression methods reveal some common redundancy in trained neural networks.
The inductive biases / regularizations that create this redundancy are investigated¹⁵
A clever optimization algorithm is created to train a network without this redundancy from the beginning of training.

Below is a table with other types of model compression and efforts to move them closer to the beginning of training¹⁶ (with varying levels of success)¹⁷:

Compression Method	Redundancy	Why?	During Training
Weight Pruning¹⁸	Many zero weights	Unclear¹⁹	Rigged Lottery¹³
Weight Sharing	Different layers tend to perform similar functions	Images are locally coherent / compositional. So are sentences.	Convolutions, Recurrences, ALBERT²⁰
Quantization²¹ ²²	Weights are low-precision	Unclear²³	XNOR Net²⁴, DoReFa-Net²⁵, ABC-Net²⁶
Matrix Factorization²⁷ ²⁸	Matrices are low rank	Dropout, Nuclear-norm regularization	ALBERT²⁰
Knowledge Distillation²⁹ ³⁰	Unclear	Unclear	BANs³¹, Snapshot KD³², Online KD³³

Future Directions

Do we really need model compression? This post’s title is provocative, but the idea is not: by tightening over-parameterization bounds and improving our optimization methods, we may reduce or eliminate the need for post-hoc model compression. Obviously there’s still a lot of open questions that need answering before we can have a definitive answer. Below is some work I’d like to see done in the next few years.

Over-parameterization

Can we get tighter bounds by peeking at the quality of the data (with low-resource computations)?
How do over-parameterization bounds change if we use a clever optimization trick (like the Rigged Lottery¹³)?
Can we get over-parameterization bounds for reinforcement-learning environments?
Can we extend these bounds to other commonly-used architctures (RNNs, Transformers)?

Optimization

Are there any other redundancies in trained neural networks that we’re not exploiting?
Make these practical:
- Training quantized neural networks from scratch.
- Training neural networks with low-rank matrices from scratch.
Figure out why knowledge distillation improves optimization. Use a similar idea to optimize while using less GPU memory, if possible.

Regularization

What types of regularization induce what types of model redundancies? (A taxonomy³ would be nice)
How is pruning and re-training related to L0 regularization? What implicit regularization induces prunability?
What kind of regularization induces quantizability?

If you work on this stuff, feel free to shoot me an email. I’d love to join (or start) a mailing list or something.

If you found this post useful, please consider citing it as:

@misc{gordon_2019,
    author = "Mitchell A. Gordon",
    title = "Do We Really Need Model Compression?",
    year = "2020",
    howpublished="http://mitchgordon.me/machine/learning/2020/01/13/do-we-really-need-model-compression.html",
}

Update 1/22/2020: Apparently Tensorflow 2.0 comes with mixed precision training out of the box now, which is pretty sick (assuming you have modern DL accelerators).

Update 4/25/2020: One of my questions has been answered by FAIR: what kind of regularization induces quantizability? Answer: just add quantization noise! Kind of a Gordonian knot answer, but still valid.

Much more on Deep Learning’s Size Problem. ↩
A common example of this is XOR which can theoretically be represented with two hidden neurons but in practice requires using around twenty. ↩
Kukačka, Jan, Vladimir Golkov, and Daniel Cremers. 2017. “Regularization for Deep Learning: A Taxonomy.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1710.10686. ↩ ↩² ↩³
Zhang, Chiyuan, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. 2016. “Understanding Deep Learning Requires Rethinking Generalization.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1611.03530. ↩
Du, Simon S., Jason D. Lee, Haochuan Li, Liwei Wang, and Xiyu Zhai. 2018. “Gradient Descent Finds Global Minima of Deep Neural Networks.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1811.03804. ↩
Haeffele, Benjamin D., and René Vidal. 2017. “Global Optimality in Neural Network Training.” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 7331–39. ↩
And it’s very active. I’ve seen a bunch of papers (that I haven’t read) improving on these types of bounds. ↩
Theoretically, though, we at least know that training a 3 neuron neural network is NP-hard. There are similar negative results for other specific tasks and architectures. There might be proof that over-parameterization is necessary and sufficient for successful training. You might be interested in this similar, foundational work. ↩
Frankle, Jonathan, Gintare Karolina Dziugaite, Daniel M. Roy, and Michael Carbin. 2019. “Linear Mode Connectivity and the Lottery Ticket Hypothesis.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1912.05671. ↩
Zhou (2019) explores this idea with more detailed experiments. Liu et al. (2018) found similar results for structured pruning (convolution channels, etc.) instead of weight pruning. They, however, could randomly initialize the structure pruned networks and train them just as well as the un-pruned networks. The difference between these results remains un-explained. ↩
Dettmers, Tim, and Luke Zettlemoyer. 2019. “Sparse Networks from Scratch: Faster Training without Losing Performance.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1907.04840. ↩
Mostafa, Hesham, and Xin Wang. 2019. “Parameter Efficient Training of Deep Convolutional Neural Networks by Dynamic Sparse Reparameterization.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1902.05967. ↩
Evci, Utku, Trevor Gale, Jacob Menick, Pablo Samuel Castro, and Erich Elsen. 2019. “Rigging the Lottery: Making All Tickets Winners.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1911.11134. ↩ ↩² ↩³
Lee, Namhoon, Thalaiyasingam Ajanthan, and Philip H. S. Torr. 2018. “SNIP: Single-Shot Network Pruning Based on Connection Sensitivity.” arXiv [cs.CV]. arXiv. http://arxiv.org/abs/1810.02340. ↩
More work is being done on deciding whether lottery tickets are general. ↩
Note that model compression is not the only path to memory-efficient training. For example, gradient checkpointing lets you trade computation time for memory when computing gradients during backprop. ↩
I would say pruning and weight sharing are almost fully explored at this point, while quantization, factorization, and knowledge distillation have the biggest opportunity for improvements. ↩
Gale, Trevor, Erich Elsen, and Sara Hooker. 2019. “The State of Sparsity in Deep Neural Networks.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1902.09574. ↩
What type of regularization induces these 0 weights? It’s not entirely clear. Haeffele and Vidal (2017)⁶ proved that when a certain class of neural networks achieve a global optimum, the parameters of some sub-network become 0. If training impicitly or explicitly prefers L0 regularized solutions, then the weights will also be sparse. ↩
Lan, Zhenzhong, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. 2019. “ALBERT: A Lite BERT for Self-Supervised Learning of Language Representations.” arXiv [cs.CL]. arXiv. http://arxiv.org/abs/1909.11942. ↩ ↩²
Here’s a survey. Other examples include QBERT and Bitwise Neural Networks. ↩
Note that quantized networks need special hardware to really see gains, which might explain why quantization is less popular than some of the other methods. ↩
inFERENCe has some thoughts about this from the Bayesian perspective. In short, flat minima (which may or may not lead to generalization) should have parameters with a low minimum-description length. Another explanation is that networks that are robust to noise generalize better, and round-off error can be thought of as a type of regularization. ↩
Rastegari, Mohammad, Vicente Ordonez, Joseph Redmon, and Ali Farhadi. 2016. “XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks.” arXiv [cs.CV]. arXiv. http://arxiv.org/abs/1603.05279. ↩
Zhou, Shuchang, Zekun Ni, Xinyu Zhou, He Wen, Yuxin Wu, and Yuheng Zou. 2016. “DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients.” https://www.semanticscholar.org/paper/8b053389eb8c18c61b84d7e59a95cb7e13f205b7. ↩
Lin, Xiaofan, Cong Zhao, and Wei Pan. 2017. “Towards Accurate Binary Convolutional Neural Network.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1711.11294. ↩
Wang, Ziheng, Jeremy Wohlwend, and Tao Lei. 2019. “Structured Pruning of Large Language Models.” arXiv [cs.CL]. arXiv. http://arxiv.org/abs/1910.04732. ↩
Denton, Emily, Wojciech Zaremba, Joan Bruna, Yann LeCun, and Rob Fergus. 2014. “Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation.” arXiv [cs.CV]. arXiv. http://arxiv.org/abs/1404.0736. ↩
Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. 2015. “Distilling the Knowledge in a Neural Network.” arXiv [stat.ML]. arXiv. http://arxiv.org/abs/1503.02531. ↩
Kim, Yoon, and Alexander M. Rush. 2016. “Sequence-Level Knowledge Distillation.” arXiv [cs.CL]. arXiv. http://arxiv.org/abs/1606.07947. ↩
Furlanello, Tommaso, Zachary C. Lipton, Michael Tschannen, Laurent Itti, and Anima Anandkumar. 2018. “Born Again Neural Networks.” arXiv [stat.ML]. arXiv. http://arxiv.org/abs/1805.04770. ↩
Yang, Chenglin, Lingxi Xie, Chi Su, and Alan L. Yuille. 2018. “Snapshot Distillation: Teacher-Student Optimization in One Generation.” https://www.semanticscholar.org/paper/a167d8a4ee261540c2b709dde2d94572c6ea3fc8. ↩
Chen, Defang, Jian-Ping Mei, Can Wang, Yan Feng, and Chun Chen. 2019. “Online Knowledge Distillation with Diverse Peers.” arXiv [cs.LG]. arXiv. http://arxiv.org/abs/1912.00350. ↩